


I. Introduction to Birthday Paradox: Probability of Coincidences, Repetition
II. Mathematics, Formula of Saliusian (Ion Saliu) Sets
III. Software to Calculate the Probability of Collisions, Coincidences, Duplication
IV. Relation of Birthday Paradox Probability to Lottery
V. Relation of Birthday Paradox Formula to Roulette
VI. Birthday Paradox and Social Security Number
VII. Birthday Paradox and the Genetic Code, DNA: Forensic Coincidences
VIII. Resources in Theory of Probability, Mathematics, Combinatorics, Formulas, Software

The BirthdayParadox software is based on the popular probability problem known as the Birthday Paradox. It is well presented by Warren Weaver in his famous book Lady Luck (page 132):
"Suppose there are N people in a room. What is the probability that at least two of them share the same birthday —the same day of the same month? … When there are 10 persons in a room together, this formula shows that the probability is 0.117 (11.7%) that at least two of them have the same birthday. For N = 22 the formula gives p = 0.476 (47.6%); whereas for n = 23 it gives p = 0.507 (50.7%)… Most people find this surprising. But even more surprising is the fact that with 50 persons, the probability is 0.970. And with 100 persons, the odds are better than three million to one that at least two have the same birthday."
The Birthday Paradox was ... born in 1938, however. It referred to fishes, of all creatures. Feels so good to be a Pisces! But this is just one element of a much bigger picture...like the fish compared to the ocean. The complete picture has the caption: "The probability of duplication or collisions". The probability of duplication or collisions is best analyzed by the mathematics of 'Ion Saliu sets'. The Saliusian sets consist of both unique elements (numbers, words) and duplicate elements. The latest software calculates also the reversed Birthday Paradox (or the reversed duplication problem). Determine the number of elements (e.g. persons, or lotto drawings) when the probability (degree of certainty) of duplication is set.
The birthday paradox resembles the pick-3/4 lottery, 1x2 soccer pools, and everything related to the sets known as EXPONENTS. Read more about all type of sets here: Calculate, generate permutations, sets, arrangements, combinations, exponents, combinatorics for any numbers and words.
My probability software PermuteCombine generates any type of sets, including exponents (111223, 111232, 123456) and combinations (123456, 123457).
The pick 3 game has the following parameters:
1) The LOWER bound = 0;
2) The UPPER bound = 9;
3) The number of ELEMENTS = 3.
In this case of exponential sets, N = 3 and M = 9 – 0 + 1 = 10. Total possible elements: 310 = 1000. The 1000 elements of the pick 3 set contain unique sets (1,2,3), plus double-digit combinations (1,1,0), plus triple-digit sets (9,9,9). The unique elements are easily calculated by using the arrangements of (M, N): 10 * 9 * 8 = 720. Yes, it is the number of trifectas in horse racing for 10 horses. If we deduct the unique sets from total elements, the result represents number of elements with AT LEAST two digits being equal. In the pick-3 case, there are 1000—720 = 280 elements with double and triple digits. Every pick-3 player knows all those sets. Obviously, the probability that at least two digits are duplicate is: 280 / 1000 = 0.28 or 28%.
The general formula of the Birthday Paradox (Collisions) is a two-step algorithm:
Number_of_Duplicate_Sets (M, N) = Exponents (M, N) – Arrangements (M, N).
The Probability_Of_Collisions (Coincidences, Birthday Paradox) = Number_Of_Duplicate_Sets (M, N) / Exponents (M, N)
Or, for 365 birthdays, Exponents (365, N) – Arrangements (365, N), where N represents the number of persons.
The interesting case is N > M. For example, dice rolling. Number of elements M = 6 (6 numbered faces from 1 to 6). If we throw 2 dice at a time, the probability of duplication (e.g. 1-1 or 6-6) is 16.66% (6 / 36). If we throw 6 dice at a time, the probability of duplication (e.g. 1-1-?-?-?-? or ?-6-?-?-?-6) is 98.46% (45936 / 46656). If we throw 7 dice at a time (7 > 6), the probability of duplication (e.g. ?-?-?-?-1-?-1 or 6-?-?-?-?-6-?) is 100% (279936 / 279936).
In such cases, the algorithm sets the arrangements (number of elements with NO duplication) to zero by default. The algorithm proceeds to dividing Total number of sets (M ^ M) to the equal value of Number of sets with duplicates [(M ^ M) – 0]. It is not a case of mathematical absurdity. It is possible to throw 7 dice at a time. But all trials will show at least two faces being equal or duplicate.
Next, the program does the necessary calculations.
Num1= Exponent(TOT2-TOT1+1, TOT3) ' all elements of the exponential set;
Num2= Arrangement(TOT2-TOT1+1, TOT3) ' non-duplicate elements (arrangements);
Num3 = Num1 - Num2 ' duplicate elements.
The calculations for: TOT1 ~ TOT2 ~ TOT3
* Total possible number of sets = Num1
** Number of sets without duplicates = Num2
*** Number of sets with at least 2 duplicates = Num3
~ The probability for this Birthday Paradox is: Num3/Num1*100 (%).
If M < N, then Num2 = 0; i.e. there are no elements without duplicates. It is the case of 1x2 soccer pools, for example. There are no unique 1x2 sets for 13 games. If the first 3 games are non-duplicate: 1,x,2, then game #4 must duplicate one of the first 3 elements.
The birthday paradox can only tell the number of duplicate sets, but not the structure of the sets. That is, 2-repeat elements are counted together with 3-repeat elements, plus 4 repeats, etc. My approach lets you determine beforehand the repeat sets by category. Look at the pick games. In the pick-3 game, M = 10, N = 3. The number of triple digit sets is equal to M (10, in this case). The number of exactly double-digit sets is equal to M * (M-1) * N (270, in this case). In the pick-4 game, M = 10, N = 4. The number of quadruple digit sets is equal to M (10, in this case). The number of exactly triple-digit sets is equal to M * (M-1) * N (360, in this case).
The user can generate the sets for the chosen parameters. The sets can be either in lexicographic order (all of them), or generate any amount of random sets. If total possible number of sets (Num1) is greater than 10,000,000 the program warns NOT to generate lexicographical sets. It would gobble up a hard disk!
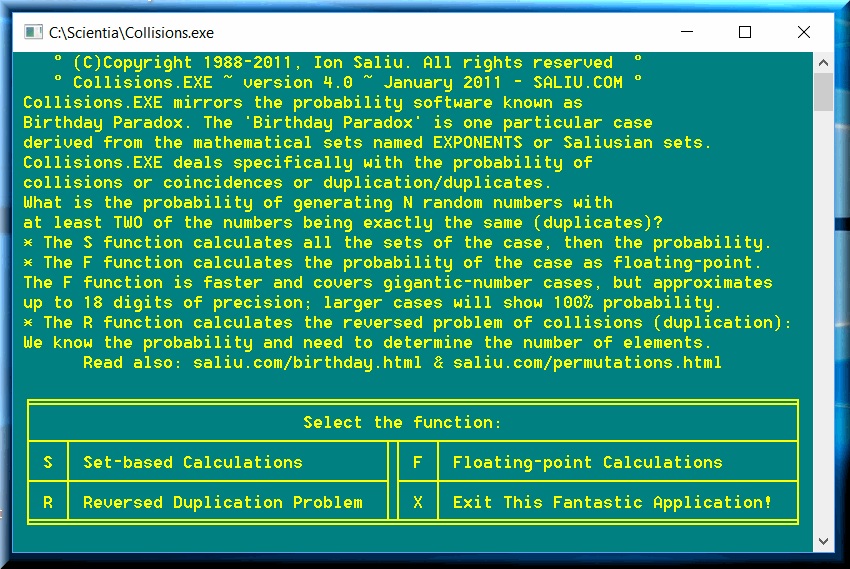
Collisions works with far larger numbers than Birthday-Paradox. I employed all the programming tricks that I know to make possible calculations for huge numbers.
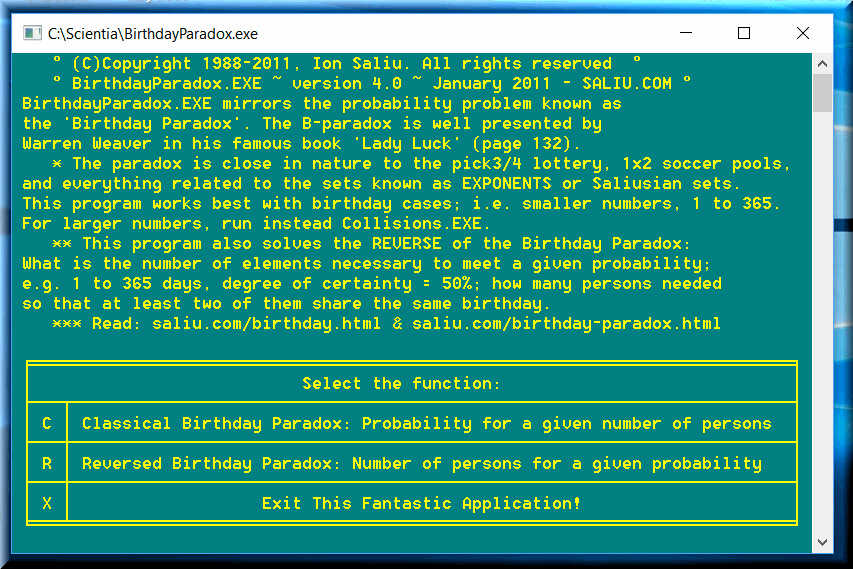
BirthdayParadox works best with birthday cases; i.e. smaller numbers, 1 to 365.
Collisions works best with larger numbers, such as genetic code sequences, lotto combinations, social security numbers, etc. Collisions, the sets-based option, is less accurate with small numbers, such as birthday cases; e.g. inaccurate for birthdays of 200 persons in the room. Collisions has a floating–point option that provides calculations with huge numbers. The procedure is accurate with an 18-digit precision. The probability beyond 18 digits is rounded up to 100%. That's the maximum of precision my compiler can trust. I urged them, badly at times, to increase the compiler precision for our era; validating the precision is the key.
I generated all 1000 sets in the pick-3 game, from 000 to 999. This Birthday Paradox application can generate all pick 3/4 sets, too. I used UTIL332 to do a statistical report (frequencies) for all 1000 combinations. Each pick-3 digit shows a frequency equal to 300, regardless of position (boxed). Thus, the probability to predict one digit is p = 300 / 1000 = 0.3 (or 30%). There is no surprise there. The probability to predict two digits is exactly the product of the two individual probabilities: 0.3 * 0.3 = 0.09 = 9%. The probability to predict three digits is exactly the product of the three individual probabilities: 0.3 * 0.3 * 0.3 = 0.027 = 2.7%. That's if we play one ticket. If we play 16 tickets, the probability grows to 43%. But, again, it has nothing to do with the 'Birthday Paradox'.
The pick-3 game has a very specific form of playing 'boxed'. In such play, 1-2-3 is the same as 2-1-3 and 3-2-1; 1-2-2 is equal to 2-1-2 or 2-2-1. The pick-3 game has 220 boxed possibilities. If we play one boxed ticket, the probability is 1 in 220 (0.45%). If we play 16 tickets, the probability is 16/220 or 7.27%. If we play all 220 boxed combinations, we are guaranteed to win!
• There are some interesting facts, however. The birthday paradox calculates that the probability to get the same pick-3 combination at least two times in 100 trials is 99.4%. I checked the most recent 200 draws in Pennsylvania Lottery. There are 34 occurrences of pick 3 straight combinations that are repeats from the previous 100 draws. There are no situations without repeats longer than 100 drawings! The birthday paradox also shows that if 100 players play independently one ticket each, the probability is 99.4% that at least two tickets have the same exact combination.
The birthday paradox applied to a lotto 6/49 game. If 10000 players play independently one combination apiece, the probability is 97.2% that at least two tickets have the same exact combination. The probability of the birthday paradox is 99.999789% if 100,000 combinations are played independently. It does not imply that the jackpot combination will be necessarily a combination played more than once! Of course, sometimes that's the case — and the jackpot is shared. Equivalently, the probability is 97.2% that at least one jackpot combination will be a repeat within 10000 drawings (something like every 100 years).
The suggestion is similar to the relation between Birthday Paradox and pick lottery games. If the roulette would draw 10 numbers at a time, the probability (i.e. duplicates). But even if the roulette game would consist of 10 spins at a time, the birthday paradox would have nothing to do with predicting the numbers. Some gamblers make the following illogical connection. If I consider 10 roulette spins at a time, in 72.7% of the cases, at least two of the numbers will be repeats. So, if I play the last 10 numbers, the chance is very good (almost 3 out of 4 cases) that one of the numbers will repeat next! Wow! That would bankrupt every casino on the planet in a few days! If the “strategy” would hold true, the probability would rise to 99.8% that the next spin will repeat a number from the last 20 spins! Virtually, play the last 20 numbers and win every time. The cost is 20 units, the payout is 36 units; therefore that player would make a profit of 16 units in every play!
The cold truth is that the famous and appealing Birthday Paradox merely shows the percentage of sets with duplicate elements in the total elements of an exponential set. That's all. So, unsuspecting roulette enthusiasts do NOT rely on the birthday paradox when playing roulette with real money. If you do, don't ask me for a refund later! Mathematically, it is correct to expect that one of the numbers in the last 26 spins will repeat next with a better than 50-50 chance. It is the median skip calculated by the Fundamental Formula of Gambling. Real-life roulette spins and randomly generated roulette numbers validate this law — always.
I did check several roulette tables in Atlantic City, 2004. I did not find a roulette marquee showing unique numbers only. Out of 15 numbers, some were repeats — from 3 to 7 repeat numbers. Problem is, the skips between Birthday Paradox situations reached 8 spins sometimes! Probably some players wait for 5 or 6 or so skips and then apply the Birthday Paradox. The average amount of unique numbers to play is 12. Must win in two spins to make a profit.
Obviously, a system as such is non-functional in a nation like China or India. Each nation has over one billion people. When the concept of SSN was devised, one billion numbers seemed sufficient to cover the population of the United States for a long period of time. But how about deaths? I hope they do not reassign social security numbers from the deceased to the living. I heard of crimes committed by using social security numbers of dead Americans. At one point, the one-billion pool will not be sufficient any more. The computers are increasingly powerful. They can handle more and more easily huge numbers. I think of a social security number in the format:
NNNN-NNN-NNNNNN
Such a number is 10,000 times greater; that is, it can cover up to 10 trillion people! The computers can handle such numbers. The numbers of the deceased can be reassigned no earlier than every million years (doubtful human species will last that long!)
The point here is to avoid duplication in relatively small groups. I receive quite a few questions related to mathematics and probability theory. Some inquirers promised that liberties, even lives were in jeopardy! How can one company uniquely identify employees without using the entire SSN #? The entire social security number is a very important privacy issue. The law penalizes the publication of the social security number of any individual. One method to respect privacy is to use only the last four digits of the SSN#. Problem is, duplication has a very high probability. There are only 10,000 possibilities, from 0000 to 9999. What is the probability that at least two persons have the exact same last four SSN digits in a group of 100 individuals? We can use our great piece of software BirthdayParadox, with the following parameters:
~ lower bound = 0
~ upper bound = 9999
~ total elements (persons) = 100.
The probability that at least two persons have the same last four SSN digits is: 39% or 1 in 2.6 (better than 1 in 3 individuals share the same last four SSN digits).
If we take into account the last five digits (0 to 99999), the probability goes way lower: 4.8% or 1 in 21 persons.
Using the new SSN format, with the last category consisting of 6 digits (0 to 999999); the probability that at least two persons have the same last six SSN digits is: 0.05% or 1 in 200. It is likely that a group of 199 persons will not have a duplication of the last six SSN digits.
I have been able to calculate the birthday paradox for the current format of the social security number. If the social security number would be assigned randomly, the repeats would be inevitable even in relatively small samples. If 100,000 social security numbers were issued randomly, the birthday paradox probability would be 99.33% to get at least one duplication. The probability grows to 99.9976% for 1,000,000 persons (virtually certainty)!
If you try to calculate the birthday paradox probability for more than 1,000,000 persons, the results are no longer reliable. The probability goes down, instead of climbing towards 100%. That's so because of the programming tricks I employed. Such tricks allow for birthday paradox calculations applicable to huge numbers. As soon as the probability starts declining, it's a sign the probability is virtually 100%. Run instead Collisions. Collisions has a floating–point option that provides calculations with huge numbers. The procedure is accurate with an 18–digit precision. The probability beyond 18 digits is rounded up to 100% (degree of certainty, however invalid philosophically, not only mathematically).
There are a few billion sequences of genes in the human genetic code — a gigantic number by normal human measure. However, that number is modest, by numerous other standards. The experts in genetics, and especially the forensics, consider that duplication of the genetic codes is almost impossible. They might say that no two humans have the same identical genetic sequences. Actually, they use a cliché such as: “The odds are like 1 in one billion… almost impossible!”
They, the modern forensics, appear to be overly religious (reminds me of a super intelligent mystic named Einstein). The birthday paradox proves otherwise. There is no God or a Super Universal Power to dispense of every genetic sequence in lexicographical order. Randomness is the highest (supreme) attribute of the Universe. All things collide (interact) randomly. Nothing comes in sequential order (lexicographic) as-if ordered by an intelligent force. That's why we haven't found any perfect shapes in the Universe, except for highly successful human attempts (e.g. circles, spheres, pyramids, cones, etc.)
The Universe is more like a gigantic lottery: All things come and go randomly. Humans are no exception. The human DNA is no exception. Every human individual gets his/her genetic sequences (DNA) absolutely randomly. Randomness implies uniqueness and repetition. I believe I know all probability formulas that calculate the degree of uniqueness and the degree of repetition for all phenomena in the Universe. All we need is to calculate all possible events (N) and all favorable cases (n).
Let's consider a very generous number of gene sequences: 10 billion (10,000,000,000 in US math). Let's suppose just one million human individuals. The probability is 99.9999% that at least two humans will have absolutely identical genetic codes! Let's take a smaller city, of only 100,000 (one hundred thousand) inhabitants. The probability is 39% that at least two humans will have absolutely identical genetic codes! It's better than 1 in 3 probability that a crime could have been committed by one of at least two persons in that 100,000-inhabitant city! Always keep in mind the at-least emphasize — and never forget the "1 in one billion" forensic statement in the court of law! Teach them forensics how to run that incredulously great and precise piece of software known as Collisions to Homo sapiens around Terra.
Keep in mind that the genetic sequences are not generated uniquely by some cosmic supercomputer. The Cosmic Supercomputer would be a more suitable metaphor for God in the third millennium. The genetic sequences are generated randomly (by Randomness Almighty, I say metaphorically). The Cosmic Supercomputer does not issue DNA (genetic sequences) based on the law or breaking the law. Whose law, after all? God's Law? If you look at all religious (sacrosanct) texts, the gods have been the most hideous of criminals! They have been the worst mass-murderers imaginable! But the gods have gotten away with crime because they have no DNA! Anyone found Jupiter's DNA? If they had discovered the DNA of Aphrodite, all rich and famous women would kill to be Aphrodite-cloned! BRRRRRRRRAHAHAHAHA.....
I want to tell you something unsettling. I sent a dozen emails or so to the most reputable organizations in the genome field. I asked them a very simple question: "How do you calculate the number of possible genetic sequences?" They all took the vow to answer any question. They are funded to answer any question. Yet, they have not answered my simple question in several years now. They never will, it seems. I'm afraid their mathematics is real bad. They feel it in their gut. My question was not meant to embarrass anybody. I wanted to help, if help was needed. I believe I am in the best position with calculating the total possible number of genetic sequences. If we know that, even closely approximately, we will know the probabilities of duplications.
It is really hard not to repeat anything in this gigantic Universe of ours. Which begs the question: “Is terrestrial intelligent life unique in the Universe?” I don't think so, coolheadedly-axiomatic one! Indeed, there is an incomprehensibly huge number of possible forms of phenomena. But there is also a huge number of already randomly generated phenomena (that exist, that is).
We apply here the by-now-famous (very well-known, that is) Ion Saliu's Paradox of N Trials. Let's say that N represents total possible cases the Universe can handle. It is even more fitting to work at a universal scale. The Universe is infinite; therefore nothing could be more fitting but consider that N tends to infinity. We know that human life exists. What is the repeat probability of human life, exactly as-is, in other parts of the Universe, when N tends to infinity? The Ion Saliu Paradox proves that the degree of uniqueness is, approximately, 63%, while the degree of duplication (repeatability) is 37%.
True, the odds against a duplication of human life, at any time, in any place of the Universe, are almost 2 to 1. But a better than 1 in 3 chance of duplication looks real good to me. After all, you or I have a chance to see the very tomorrow worse than winning a 5/37 lotto game (I say it on Augustus 3, 2008)! Read the Probability Caveats page — I am sure you will, with a high degree of certainty... we'll be here again... tomorrow! Thus, the probability of duplication of intelligent life is quite high in this Universe as it was in a previous Universe or will be in a future billions-of-billion-year Universe. It's mathematical.
It is time now for this yours truly Pisces to go back to work for his boss, Neptune. Beware, pirates!
Read Ion Saliu's first book in print:  Probability Theory, Live!
Probability Theory, Live!
~ Discover profound philosophical implications of the Formula of TheEverything, including the Birthday Paradox and repetition of phenomena, Life included.


Home | Search | New Writings | Odds, Generator | Contents | Forums | Sitemap
